Статья о том, что такое дробно-линейные преобразования в комплексной плоскости могут пригодиться в жизни и как при помощи них можно искажать объект для получения желаемого вида. В конце бонусом получим анимацию :).

В целом, дробно-линейные преобразования на комплексной плоскости -- это преобразования вида , где a, b, c, d и z -- комплексные числа. Но об этом позже. Начнем с самого начала:

Допустим, у нас есть кот 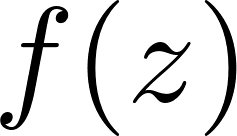. Поставим этого кота на комплексную плоскость.

Что можно сделать с этим котом? Самое простое - сдвинуть кота по какой-либо из координат вправо/влево или вверх/вниз. Для этого надо прибавить к коту какое-либо комплексное число. Получим отображение вида: , где a - комплексное число.

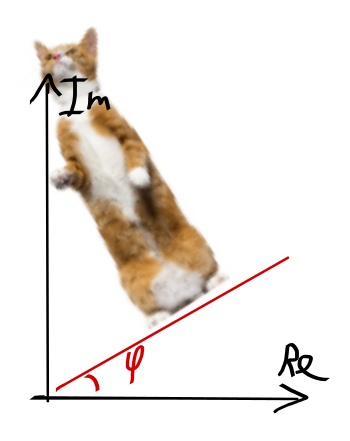
Помимо этого, можно повернуть этого кота на некоторый угол  .  .

И увеличить/уменьшить кота в k раз:

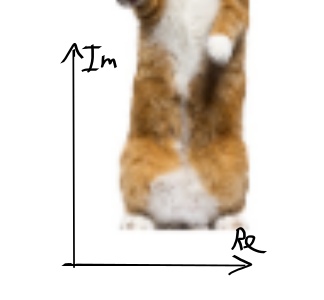
На этом линейные преобразования закончились. Комбинируя эти 3 преобразования можно уже добиваться интересных результатов и располагать кота в любом положении и, например, закрутить кота в спираль.

Для того, чтобы сделать анимацию, представленную выше, достаточно уметь передвигать кота в плоскости, поворачивать его и уменьшать размер с каким-то определенным шагом, применив к коту функцию 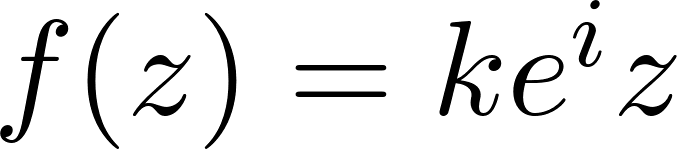 .  Но все это выглядит неестественно, будто анимация, созданная из фотографий рисунка кота, которого каждый кадр перемещают по спирали. Для того, чтобы сделать изображение реалистичнее пойдем на одну хитрость - а именно, инвертируем кота.

Применим преобразование 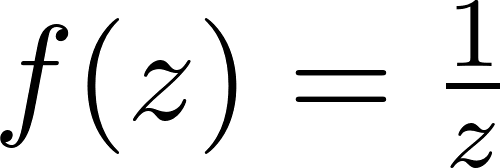 к коту: после этого кот будет инвертирован относительно единичной окружности. Та часть кота, которая была за окружностью, окажется внутри нее, а часть, которая была внутри -- снаружи.

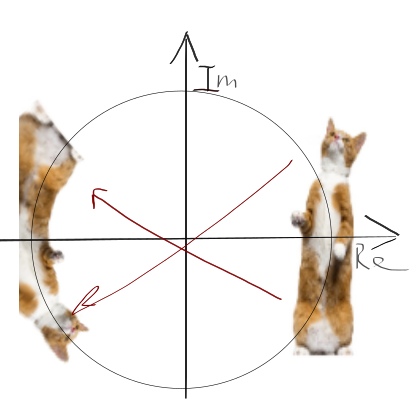
Ну вот, теперь кот при повороте по спирали поворачивает тело за счет того, что та часть кота, которая находилась снаружи от единичной окружности оказалась внутри в сжатом виде, а часть, бывшая снаружи -- внутри в сжатом. Правда, кот начал крутиться в другую сторону: это также произошло за счет инверсии. К тому же, чем ближе кот находился к центру спирали, тем дальше от спирали он будет находится при инверсии и тем больше искажение формы.

Спираль сворачивается в точку 0, а начинает разворачиваться с . Дробно-линейное преобразование переместит точку, с которой раскручивается спираль в -1, а точку, в которую спираль сходится -- в 1 (). Как-то так:

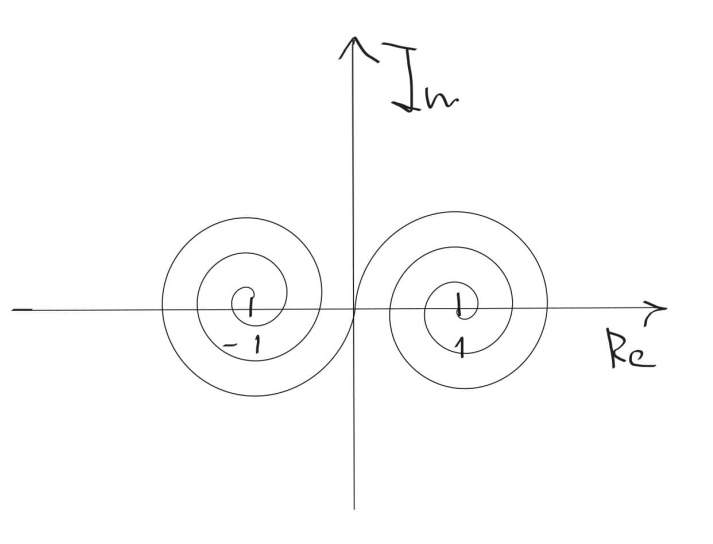
По каким еще траекториям можно перемещать кота ограничивает только фантазия.